The polar planimeter
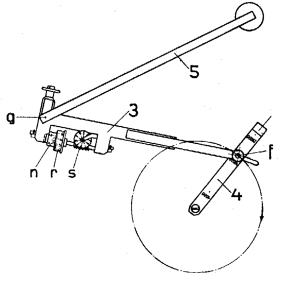
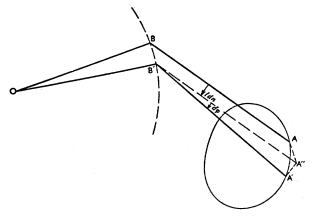
The arm OB (first figure below) has a pivot point in O which is fixed to the paper. In our Siemens planimeter (top figure), O is a sharp point pressed into the paper by a weight.
Point B, which can describe a circle around O, rests in turn on a point of the arm AC. Point A is is moved by the user along the curve drawn on the paper. The other end of this arm rests on the paper with a steel wheel W, the axis of which is accurately parallel to AC. (In the Siemens planimeter, W is on the other side of A; also there is a supporting wheel perpendicular to W). The rotation of W can be measured accurately with the help of a division on its rim and a revolution counter. If AC is moved in its own direction, W slips over the paper without turning. However any movement component n normal to AC leads to a proportional rotation of W.
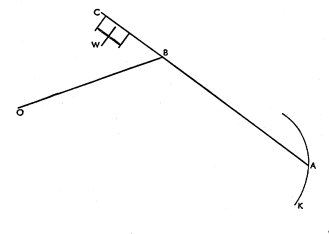
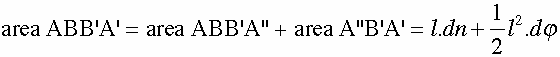
If A makes a complete roundtrip over the closed curve K, then the surface covered by AB is equal to
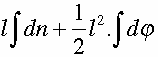
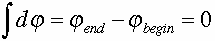

Two polar planimeters: Siemens & Halske (made by A. Blankenburg), Germany ~1930 and Allbrit/Stanley, UK 1950.
Inset bottom left: detail of S & H planimeter mechanism.

Reiss compensation polar planimeter 3005 (DDR, 1969)
References: this explanation was adapted from the ENSIE encyclopedia (Amsterdam 1949). The top picture was taken from our Siemens Spezial-Planimeter manual (Berlin 1928).
Prof. Dr. Joachim Fischer (München) provided a number of corrections and additions.
A mathematical treatment of the planimeter, based on Green's Theorem, is given in this Wikipedia article.
